Kelly Krumrie’s figuring
On Fractals, Part 1
Figuring is a monthly column that puzzles over (to figure) and gives shape to (a figure) writing, art, and environments that integrate or concern mathematics and the sciences. This month’s column looks at the connection between language and fractals.
I’m working up to something, but I don’t quite have it yet. Maybe like a fractal I’ve got a self-same pattern on my mind. Meaning, iterations of similarity. Picture an idea multiplying toward a center but out of reach.
I keep coming upon fractal as a metaphor in writing and as a kind of analogy in literary criticism. I’m researching the intersections of mathematics and literature, so this isn’t surprising. But I’m finding fractal in / on works that have little to do with mathematics, and sometimes the concept’s not necessarily applied correctly. That is, I am not confident folks actually know what a fractal is.
One of my questions is does it matter if I know what a fractal is when I use it.
In criticism, fractal can be a good description for a formal trait. Repetition in texts is fractal, and so is memory, and so are time and space and their representations. Identity iterated. A fractal feeling.
I’ve been writing about literature this way too. I’ve got a lot of questions. To move toward answering them, I’d like to look at two things, which I will split into two entries for this column. Simply:
Part 1: What is a fractal, really?
Part 2: How can literature be fractal, and why might we describe it as such?
[Spoiler: Lisa Robertson’s new novel, The Baudelaire Fractal, reignited my questions from a critical article on Gertrude Stein’s use of repetition as fractal, so that’s likely where I’ll go. But if you have other suggestions for fractals in literature, please send them my way (here or Twitter / Instagram: @syntacticon).]
*
We know fractals from snowflakes, wild Trapper Keeper patterns, interactive Mandelbrot set computer programs my eighth graders would zoom into endlessly, curls and colors, diving into Seahorse Valley, faces close to the screen until I gently pulled the mouse away.
Here is how to draw one:
draw a straight line, no less than about two inches
[so you have enough space]
divide the line into three equal parts
label the extremities and segments of the line A, B, C, D
[extremities just mean ends and segments just means the points where you divided the line]
using line segment BC as a base, draw an equilateral triangle
label the top of this triangle E
divide line segment AB into three equal parts
label the center segment FG
using line segment FG as a base, draw an equilateral triangle
[keep this triangle on the same side of the original line as the first triangle: like, they should be pointing in the same direction]
label the top of this triangle H
divide line segment BE into three equal parts
label the center segment IJ
using line segment IJ as a base, draw an equilateral triangle
label the top of this triangle K
continue for line segments EC, CD, and so on
If you keep going (and you can even start working off the original line as the side of a bigger triangle), you’ll get something like this, which becomes the Koch snowflake fractal.
I am fascinated by the rendering of geometric constructions in language, the Euclidean inquiry into what is a line and how can I both draw and describe it, and with what tools… How this writing is similar to and different from poetry, for example. How the directions above make something by doing the same thing over and over.
The word fractal wasn’t coined until 1975 with fractional used in a fractal sense in 1967, both by Benoit Mandelbrot. Its Proto-Indo-European root, via the Latin fractus, means break, and it’s related, of course, to fraction, fracture, and fragment, but also fragile and frail.
Thinking about writing mathematics and writing (about) poetry and prose involves a recognition of the limit of what we can say and how.
A fractal, most simply, “is an object or quantity that displays self-similarity… on all scales. The object need not exhibit exactly the same structure at all scales, but the same ‘type’ of structure” (WolframMathWorld). In the Koch snowflake, you keep dividing lines into thirds and drawing triangles, and the sides of the triangles become lines on which you draw more triangles, tiny ones and larger ones, on all scales, infinitely.
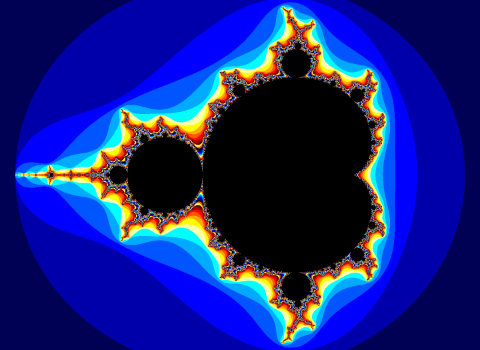
Fractals have geometric representations (like a series of triangles) but can also be written as equations. Plotting a certain series of equations on a graph can make an image like this:
This fractal is generated from the Mandelbrot set. The set is a series of equations that repeat. The output of one is the input for the next. When plugged into a graph, it makes this picture. With a computer program (or you can just find YouTube videos), you can zoom into the finer parts of the image and see more and more patterns, this same one and other swirling related shapes, in an array of colors. It’s really pretty engrossing, and the math behind it is complicated. This video from Numberphile is one of the clearest explanations I’ve seen, even though the presenter skips over complex numbers which I haven’t yet gotten my head around.
In the video, he describes the black portion in images like the above as “a geography of iterative stability.” The colors outside the main shape indicate levels of instability. Stability is whether the equations hold, or something, this is where it loses me (you can watch how he manipulates the graph in the video)… but the point is: what a phrase: geography of iterative stability.
I see why someone would want to write this, to generate repetitions of scale, to create an unfolding landscape, a language of in/stability. I want to write it. It’s hard to resist. And for a reviewer or critic describing complex writing, a layered or fragmented narrative, something splintering off and returning, folds, levels of frailty…
*
In considering all this, I am wondering about the limits of analogy: from the relationship between mathematics and language to the formal potentials of fractal forms, translated into word, image, or scene. And what are our responsibilities as readers and writers? To understanding? What loyalties to the equations or shapes?
*
In Part 2, I hope to tease out answering these questions by looking at literary examples that potentially are and criticism that uses fractal.

About the Author
Kelly Krumrie‘s prose, poetry, and reviews are forthcoming from or appear in Entropy, La Vague, Black Warrior Review, Full Stop, and elsewhere. She is a PhD candidate in Creative Writing at the University of Denver where she serves as the prose editor for Denver Quarterly.