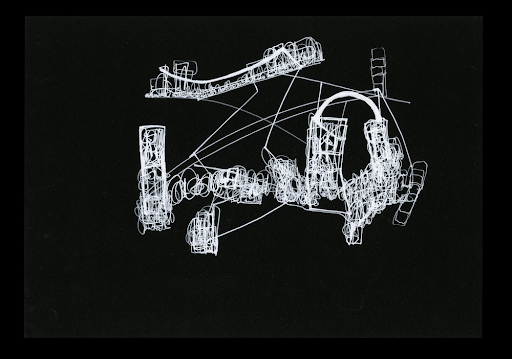
*

In conversation with Fred Moten about her new collection of drawings, One Long Black Sentence, for which Moten writes an “anindex,” Renee Gladman asks, 

When is an index?

In the collection, the anindex is at the end. Rectangles of prose at the bottom of blank, black, landscape-formatted pages. Moten riffs on index’s connection to “point”— the action, to point; your index finger—and the geometric point, which makes a line, writing in the anindex:

There is, on the one hand, the nonidentity of the point and line. There is, on the other hand, this sense that the line points. Is a line a continuous series of point(s) that points?

The opening of the first of Euclid’s thirteen books of The Elements begins with the definition on which all of his geometry is based:

1. A point is that which has no part.

Then:

1. A line is breadthless length. 
2. The extremities of a line are points. 
3. A straight line is a line which lies evenly with the points on itself. 

The point is a starting place and an end; it has no dimension. Neither does the line: a series of points. A point is a location; a line is an idea. The point and the line initiate. 

As for Moten’s “nonidentity of the point and line,” he writes earlier, 

Is there a non-deictic index, some kind of curved or displaced pointing?

Geometric proofs are non-deictic. They take place in no space or time: abstract truth writ crystalline. Though, The Elements are a container, a kind of space; each proof builds from the one before it—beginning with point. There is a temporal origin, then, if you think that definition is a sufficient launch. An eternal, an infinite origin? Only in writing?

Then there is Euclid, the person who, like Pythagoras, may have been a group of people, or no one. The text of The Elements is biblical in its assemblage, transcription, annotation, legend. Even Hypatia wrote in the margins. 

Further, constructions in proofs use the imperative mood (an eternal present tense): Describe a circle. Draw a line. Bisect the angle. 

Imperatives point to you. Me? Anyone?

Who is doing the writing, and who is constructing the proof later, in their minds or with their pencils? The imperative in a geometric construction requires a removal from the page toward an action on another. 

In the conversation, Gladman says, 

That’s what writing is—an avatar for the body to live out thinking.

Math is thinking in writing, just a different kind of writing. The avatar in proof-writing is also the imaginary person doing the proof, the one the proof writer is writing for: anyone who follows the directions: me. 

The drawings in One Long Black Sentence are writing-writing, thinking-writing, drawing-writing, building-writing, city-writing, math-writing. They take place in no time or space, especially on the black page. I am looking at the bright white lines in outer space and in the belly of the earth and in a darkness I can’t define. I’m alone with them, or inside, or not in any place. My eyes go inside, thinking with my mind’s eye. Gladman and Moten talk about dimension; Gladman says,

The hint of writing also troubles the flatness because writing is another kind of vast space.

Even for the mathematician in the translation from imagination to transcription. A line is breadthless length. 

Later in the collection, watercolor and pastels introduce a new, shifting flatness on what Moten calls the blackground. The black page is two-dimensional; Gladman’s drawings create depth. This is both deictic by pointing to a position and non-deictic in that the position struggles to exist. Moten says, 

How do you create richness in the flat? How do you create richness and thickness when they’re crushing us all the fucking time?

The drawings fold back on themselves. Symbols that look like equations hover like satellites. Buildings made of overlapped writing and uneven prisms are tethered together by single lines, like electrical wires or multidimensional clotheslines. 

Read the drawings in more than one direction. What is the sentence in/to these lines? A sentence is also a length of time. 

A triangle isn’t itself sayable, but color is a kind of imperative. 

Ravicka has yellow air. Points, lines, planes, grids, and cubes in real or imagined spaces and dimensions are all over Gladman’s prose—just flipping around to what I’ve circled over the years (another dimension). Her texts and drawings are not proofs or formal geometry, but they point to it, are indexical to it. 

The imperative in a geometric construction requires a removal from the page toward an action on another. When is an index? Now? 

*