Kelly Krumrie’s figuring
Any Viewing Demands Imagination
Figuring is a monthly column that puzzles over (to figure) and gives shape to (a figure) writing, art, and environments that integrate or concern mathematics and the sciences. In this 2022 edition, Krumie discusses Mel Bochner’s Drawings: A Retrospective at the Art Institute of Chicago (Apr. 23–Aug. 22, 2022) & Renee Gladman’s Plans for Sentences (Wave Books, 2022)
Kelly Krumrie’s figuring
Any Viewing Demands Imagination
Figuring is a monthly column that puzzles over (to figure) and gives shape to (a figure) writing, art, and environments that integrate or concern mathematics and the sciences.
When I first read Plans for Sentences, I felt like I was missing something because I was: the sentences in the book aren’t the sentences but plans for potential sentences, or plans for a relationship between a sentence and a drawing, or a drawing as a sentence—this last probably closest to my understanding of Renee Gladman’s prose architectures broadly. So missing something is part of it: an absent referent, or a referent at the edge of my vision, tangled in the line of itself. Shortly after reading it, I saw a retrospective of Mel Bochner’s drawings at the Art Institute of Chicago. While I was looking at the drawings and thinking about them later, I wondered if Bochner could help me figure out Gladman. There was something in his geometry, or appeals to geometric forms, numbers, mathematics, and language that reminded me of Gladman: the sense of measurement and literal measurement—often a measurement of nothing. I’ve probably said somewhere (here or tirelessly to people who know me) that sentences, of course, are like a form of measure. They’re a unit, a categorical organization, that weighs one thing (an idea, a thing in the world, the world) against another (words in their order).
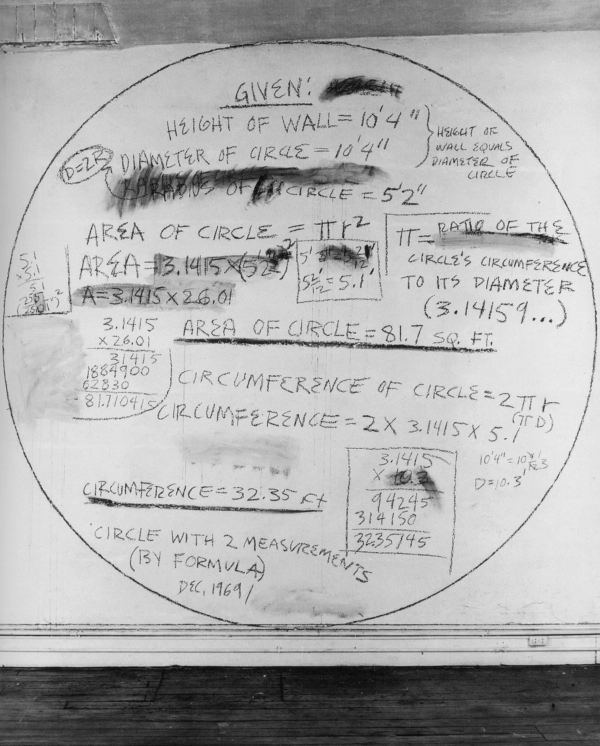
Circle with 2 Measurements (By Formula), 1969/2022 by Mel Bochner
More: Measurement is, at its core, a comparison between two things. There is the standard of measurement and the thing you’re measuring against it. There is the ruler, an object, that has little marks on it, and these marks are numbered, and the marks align with what we’ve decided the ruler will mean, that is, in the U.S., inches, twelve of them, the whole thing broken up into smaller increments and measuring a foot in total. A pencil is whatever size it is when I set it next to a ruler: the size is the number on the ruler. I’ve written and talked about this concept before—it and its relationship to poetry. It’s simple and unsettling and I could go on.
Take a look at the header image for the Bochner retrospective on the Art Institute’s website. Many of the drawings collected there are only measurements: measurements for potential projects or just the shapes he’s drawn themselves. Scroll down the page; there are a few more. In one, he’s drawn a pile of stones and numbered them. Others are three-dimensional renderings of rooms and things that could be in the rooms. There’s graph paper and hatch marks. Measurement’s all over the place; he’s written and spoken about it and even has a series called Measurements. You can see more examples here. The Art Institute exhibit is wildly mathematical, including drawings of geometric shapes, but the fun part is this thinking about measurement and the occasional absence of any object: measuring what?
Here’s Bochner:
Measurement is an operation. Its commonness of application renders it virtually invisible. Measurement is one of our means of believing that the world can be reduced to a function of human understanding. Yet, when forced to surrender its transparency, measurement reveals an essential nothing-ness. The yardstick does not say that the thing we are measuring is one yard long. Something must be added to the yardstick in order that it assert anything about the length of the object. This something is a purely mental act… an <>. If we subtract this assumption (avoiding any connotations of irony), what is left?
The relationship between Bochner’s work and language is clear if you do a quick Google image search. However, most of this retrospective, or at least my memory of it, didn’t include much of his word work. There were a few lists, and images were labeled, kind of diagrammatically, but overall the collection felt more like mathematical drawings to me than conceptual language paintings. But that’s not entirely true. A particular number/graph series that included quotations from Wittgenstein held me to it. I’ll come back to that in a minute.
Gladman’s Plans for Sentences uses facing pages to pair a drawing—more of her prose architectures—with descriptions for sentences. These are sentences themselves, but they’re not the sentences—those sentences, the ones being described, don’t yet exist and are at the same time renditions of the drawing the plans face. The drawings are and are not the planned sentences. They are also not the descriptions; or, rather, the descriptions are not descriptions of the drawings necessarily. The written sentences are also alphabetically indexed in the back of the book. This is all a kind of measurement. Do you see what I mean? The drawings, asemic and architectural, gestural, a little mathematical (I wrote about this here), are not a unit of measurement, I don’t think. Neither are the unwritten sentences, neither are the descriptions of sentences and/or drawings. The work refracts, and I mean this almost literally.
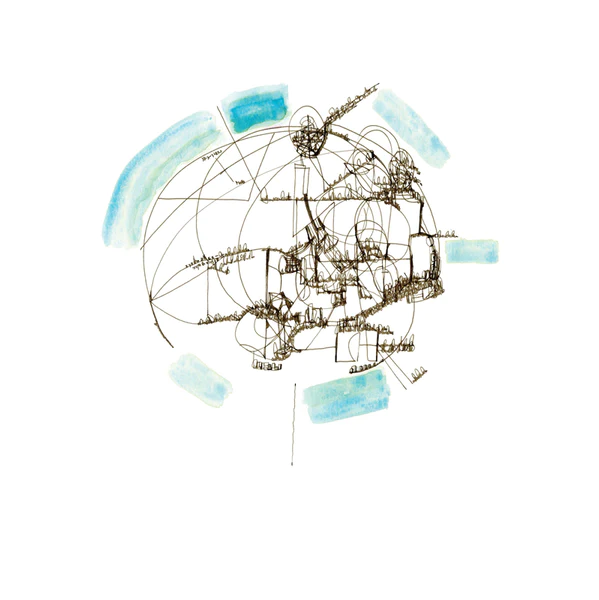
Territories of the Poem, 2017-2018 by Renee Gladman
I’m not sure I can summarize the content of the sentences Gladman has written. They kind of swoop around and tangle, not unlike the drawings themselves. But some of the sentences refer to mathematical concepts, which is not completely new or rare to appear in Gladman’s prose. For example:
Fig. 40: “This chapter will slide into your math diaphanously and will make a memoir of your space problem: the concentric to the grain upon the slope to the stacked.”
Fig. 49: “These sentences will drop the nominative as a translation of sticks, geometrically, and will pull the number to the letter, will pour texture on the plain and crust the chapter // This chapter will comprise 465 passages without words; and there will be a gray happening”
Think now of space problems and slopes, how math can slide diaphanously. These moments made me think of grid paintings (“a translation of sticks”) and labeled diagrams (“pull the number to the letter”)—which is a bit of what Bochner gets up to. They also reminded me of a moment from Gladman’s Calamities. The speaker is talking with her students about reading poetry by Ed Roberson:
I was going to try to draw a grid of light [on the whiteboard], as if one were looking down upon it, a grid that extended across an opaque surface, then draw, a good distance below that, a container, inside which were symbols. From the lower container, I wanted to draw lines that reached the opaque surface then became the actual lines of the grid. I would call those lines emanations. Without being essentialist, or perhaps being only momentarily so, I wanted to say, Often when reading poetry, it’s the grid you’re experiencing, and the grid is not the same thing as that subterranean container, where some meaning might lie, the actual story of the poem, rather it’s the shape of the emanations refracted through language and feeling (though many contemporary poems have no feeling) that you’re reading. I didn’t know how to draw the effect of looking down on something, so I asked for a volunteer. Someone tall offered, and as I was looking up at his attempt to look down, I realized that there was a flaw to my thinking. The place from which the emanations arose was not intact, it was not a container wherein lay meaning. It was a grid itself but of what I could not explain within the allotted time. I had to let the class go: it was 3:51, one minute into their “free” time. I couldn’t find my words; they remained sitting there. How could I send them off to read Roberson’s book without having explained poetry to them. “There is a grid above and a grid below” I said slowly, trying not to uplift my voice into a question. Perhaps to read poetry was to read through a sieve. I wanted to incorporate the idea of a matrix. “Poetry comes out of nothing,” I said, opening something I would never be able to close. 3:52. “Read the nothing,” I shouted after them as they walked out the door.
There are a few places to go from here. The prose architectures aren’t grids but they have a linear ground: since they’re cities (or described as cities, architectural spaces), they often include a horizontality across the page at the base of the image: a ground. Many, though, are fairly two dimensional, so there’s a flatness, like a grid. This flatness is expansive in her collection of drawings One Long Black Sentence where the drawings are printed in white ink on black paper: the black paper magnifies the density of potential depth. Fred Moten describes this as “richness in the flat” in a conversation with Gladman.
Gladman’s appeal to “read the nothing” in the approximation of a grid that is poem, or poem as a series of grids, or grid as sieve, got me thinking about the measurement of absence, which is a bit of what Bochner does. He measures rooms, sure, and pieces of paper, but what are these and why? He says in an interview that the work is more of an idea than a thing you can hold: the stickered numbers on the wall don’t matter but that the wall is measured. The work can be transferred, recreated, following a set of instructions. Not all of it, but some of it. He draws a circle on the wall and the measure of the circle is the thing. I’m curious about mathematical gestures in visual art and their relationship to information: what you get out of what’s measured. What’s taken away? What is it that I see? Know differently? Know better?
John Elderfield: “Grid painting is generally only cumulative when its units are informational containers like Warhol’s; and it is not quite a tautology to suggest that when such painting does use a cumulative method it somehow demands that it be ‘read’ in an informational way. The grid as a ‘containing’ framework is of obvious relevance here.”
Rosalind Krauss: “Unlike perspective, the grid does not map the space of a room or a landscape or a group of figures onto the surface of a painting. Indeed, if it maps anything, it maps the surface of the painting itself. It is a transfer in which nothing changes place.”
James Elkins: “A gridded picture by Agnes Martin doesn’t measure anything, and it only makes an indistinct reference to the concept of measurement. Marie Krane’s offset grids are not made to measure anything, just to propose that something is measured, or—to put it in affective terms—to elicit the feeling of measurement.”
Each of these suggests that grids are for something, that there is some other set of measurement, another thing that the grid is being used for, in service of something else, to get or see other information, a tool, really, and what many of these artists do (Elkins writes about this well) is remove this other thing, the referent, and leave the measurement hanging.
What Gladman and Bochner do, though, and slightly differently from each other, still, is tie this information, this “missing” or other thing, to language—and to that end, language that isn’t there.
I’m trying to negotiate the relationship between language present and absent, mathematical and otherwise.
We don’t usually expect abstract art to be informational, but we might expect, to some extent, math to be. But math is a curious case of ultimate facticity and ultimate absence.
Peter Janich: “When geometry, for instance, is operationally justified, you find yourself no longer talking about the description of the actions of producing spatial forms or tracing figures; rather, these actions are actually concretely carried out, operationalized, because otherwise the objects in question would be inaccessible and their hypothetical fiction would lose any relation to reality. Implementations make the objects belonging to the reality in question available for use.”
Janich is writing about “information,” but his point here about geometry is apt. It’s not what geometry yields but the act of doing it that creates / is the information. The use of the tools. Philosopher of mathematics and semiotics Brian Rotman writes something similar, essentially, about mathematics more broadly: that math exists only when you’re doing it, when you’re working the problem, writing it all out. He goes so far as to say math is only writing. It is its activity, drawn out. Similarly, classics scholar Reviel Netz writes about the relationship between the written words of Ancient Greek geometric proofs and their accompanying diagrams. (It’s worth noting that I came to Netz via the poet Jay Wright who is in my thinking somewhere here too, but I haven’t been able to find out where / how yet.) As I was reading Plans for Sentences, I was also thinking of these ideas of Netz’s: the writing on the right page as proof and the drawing on the left page as diagram.
Netz traces the Greeks’ use of diagrams (many of which are lost) in relation to the text: which comes first? Which is dependent on which? Do the proofs describe the diagrams or do the diagrams provide more information for the proofs? Here are a few snippets from Netz:
“The limitations of the media available suggest, rather, the preparation of the diagram prior to the communicative act—a consequence of the inability to erase.”
“Any viewing demands imagination.”
“This has the surprising result that the diagram is not directly recoverable from the text.”
“The important general observation is that the diagram sets up a world of reference, which delimits the text.”
“Each geometric proposition sets up its own universe—which is its diagram.”
“The diagram is not a representation of something else; it is the thing itself. It is not like a representation of a building, it is like a building acted upon and constructed. Greek geometry is the study of spatial action, not of visual representation.”
The diagram and the proof exist simultaneously even though, as he suggests, the diagram may have come first in practice. Now left with only text (the diagrams may have been drawn on walls or on the ground), many diagrams cannot be recreated: the text isn’t a sufficient description of the drawing. But the proof (the text) isn’t intended to be a description of the drawing but rather a set of actions taken out to render and/or understand something from the drawing. The drawing is, as he says, acted upon via the proof, via the mathematician doing the work: an imaginative, linguistic, and artistic act. There is, then, an operation in the gap.
To take this idea one step further, in a press release for a show titled “Drawings” in 1969, Bochner writes,
“Diagrammatic drawings” differ… in terms of purpose. If the artist’s intention is to have a professional carpenter, metalworker, painter, or photographer fabricate the final state of his work, he must be able to “describe” accurately his ideas in the graphic language of that profession. Numerous standardized methods of notation exist to ensure the error-proof decoding of ideas. Flattened projections can then be “decompressed” or “real-ized” as objects. Although schematic drawings must be concise and unambiguous, they will convey no information to the observer uninitiated in the particular code involved. Diagrammatic drawings are also useful in the mapping of systems, plotting and recording of data, or conveyance of information pertinent to installation of works having multiple components. Drawing is a language.
This is getting a bit at replicability, sets of instructions: the diagram as tool. Drawing plans are meant to be used for recreation, explicit direction, even more so than the proof. The proof and the geometric diagram are entangled; the diagrammatic drawing is its own proof. Or, rather, it becomes itself when it’s recreated in the world? Geometry is when I do it; a diagram is when I use it? Here, “drawing is a language” relates to this idea of information: a sentence is telling me something. A sentence tells me something differently from how a drawing tells me something, any drawing, including geometric and diagrammatic ones.
At the Bochner retrospective, I spent most of my time looking at a few drawings from the 1973 series “Counting Alternatives: Second Readings (Rotations)” also known as “The Wittgenstein Illustrations.” This series consists of lithograph prints of a square with vertical, horizontal, and diagonal axes on which Bochner has written numbers. Each has a quotation from Wittgenstein’s Zettel in the bottom left corner. The numbers follow one or several of the axes, from 0 to however many fit on the line. For example, in one, numbers line the top horizontal line of the square and read, from left to right, 0 to 42. In another, 0 through 50 are written along the y-axis from top to bottom. The number lines, over the thin, faint, axis lines, form angles, Xs, and asterisks. (You can see a few of them from 1991 on the Met’s website.)
The one I hung around longest has numbers along the axes in an asterisk shape, but not the one you can see online; I haven’t found an available picture of it. My photo from my visit is blurry, cut off at one edge, and there are reflections of light in the frame’s glass. The numbers along the y-axis, again descending from the top, go from 0 to 25 with 26 in the center, at the axes’ origin, then each of the other lines (along the remainder of the y, the x, and the diagonals) begin from there, from the origin, at 27, and extend in their respective directions ending in 58, 48, 58, 50, 59, 50, and 58, going clockwise from the 0 at the top of the y. Actually, I see now that the 0 is outside the frame of the square, just above the beginning of the y-axis’s line, though still in line with it. In fact, looking at the 1991 series on the Met’s site and the 1993 series on the Art Institute’s site, all of the 0s are outside of the square, just out of line with the number line. I don’t have pictures of the entire 1973 series on view in Chicago, and the exhibition catalog is too expensive for me to buy and not at the library, nor can I find them online, so I can’t, at this moment, be sure if all the 0s there are also outside, or if I’d have anything to say about it if they were. Back to this one: The 27s form a kind of circle around the 26. The numbers are even in size but still handwritten, and they’re clearly not perfectly measured out as the lists don’t end with the same number. That is, it seems that Bochner proceeded to write the numbers starting from the center and stopped when he reached the end of the line at the edge of the square. It’s the fact that the numbers don’t line up: you might not notice it. The numbers don’t really matter, then. They aren’t measuring the space or even naming it. A square, with perfectly proportioned axes, is even, but these numbers aren’t even though they’re on it.
The Zettel quotation for this piece reads:
#572: Isn’t there something here like the relation between Euclidean geometry and the experience of the senses? (I mean that there is a profound resemblance.) For Euclidean geometry too corresponds to experience only in some way that is not at all easy to understand, not merely as something more exact to its less exact counterpart.
Euclidean geometry is geometry extended from (you guessed it) the work of Euclid, meaning a set of axioms and propositions proceeding from those axioms, primarily on / about two-dimensional geometric relationships (though he does go into solids and conics in later works). Zettel was published posthumously and is a piling together of slips of paper Wittgenstein had stored in a box (zettel meaning cuttings or slips). Some were bundled together, and others were left loose. Folks who compiled the slips into the book we have now organized them as best they could by proximity and topic. To say, the excerpts Bochner pulls and writes at the bottom of the prints are fairly standalone so there’s not much else to go on by looking at, for example, #571 or #573. Obviously I can’t go on about Wittgenstein or even twentieth century visual art—there are other essays and books by people more qualified than me, it would take forever, and even within this narrow scope there are at least six other tangents I could putter along from here (e.g., see Zettel #201 or #438). I’ve followed my thinking down this line and I’m trying to bring it back to Gladman. Clearly, though, in #572, what Wittgenstein is pointing to is the complexity in what appears to be abundantly clear: a straight line can be as fuzzy as feeling or thinking.
It’s the same with measurement, I’d argue. I think measurement can be a feeling, like Elkins says, a suggestion of something that slips through my thinking of it. An agreement too, Bochner points out elsewhere (and I’ve quoted above): measurement is an assumption about an agreement to standardization. See also Gertrude Stein in “Are There Arithmetics”: “How many are there of hats and hats… how many are there… and who says so.”
What’s happening in Plans for Sentences is what Netz is describing in the relationship between the proof and the diagram: “Any viewing demands imagination.” The drawings here, her best yet, ignite my imagination with even the briefest viewing: I’m pulled into them and away from the other part of the work. Still, there’s something to be done between the facing pages, or off the page when thinking, when I look up and stare out the window. I’m wrestling a little with the text itself because the sentences are exploratory and rich, in many moments surprising and strange, but the system set up by the book presents a somewhat diagrammatic expectation, a negotiation among parts. I have two sentences on Stein by Sianne Ngai written down nearby, and I don’t think either Plans for Sentences or Bochner’s drawings are particularly Steinian, but Ngai’s descriptions feel transferable. One is “the tension created by slightly overlapping sentences results in a gap,” and the other is “language that threatens the limits of the self by challenging its ability to respond.” Plans for Sentences’ overlappingness of image, sentence, index, and potential / absence, I’ve already said, is like this gap in the grid: the gap in a grid painting, the gap in Gladman’s own description of poetry. Sometimes, though, I think the gap in the grid can be too wide. Part of the tension’s in what’s missing, but it’s on the edge of leaving me with not much to hold on to—and what I’m not sure about is where the line is. I’m looking for the assumption, some kind of ruler, or something in the world to stretch against the rulers I’ve been given. The same can be said for many experimental / conceptual works, of course. But, actually, this vagueness works well for art that engages with mathematical ideas because math is, in a lot of ways, nothing. It’s only there when it’s being done. It’s kind of all signifier, which challenges my own ability to respond, me looking for the Euclidean line in all this, knowing that I should know better than to try lining anything up with it.
Bibliography:
Bochner, Mel. Solar System & Rest Rooms: Writings and Interviews, 1965-2007. MIT, 2008.
Elderfield, John. “Grids.” Artforum, May 1972, https://www.artforum.com/print/197205/grids-36215.
Elkins, James. Six Stories from the End of Representation: Images in Painting, Photography, Astronomy, Microscopy, Particle Physics, and Quantum Mechanics, 1980-2000. Stanford UP, 2008.
Gladman, Renee. Calamities. Wave Books, 2016.
Plans for Sentences. Wave Books, 2022.
Janich, Peter. What Is Information?, translated by Eric Hayot and Lea Pao, University of Minnesota Press, 2018.
Kraus, Rosalind E. “Grids.” October, vol. 9, Summer 1979, pp. 50–64.
Netz, Reviel. The Shaping of Deduction in Greek Mathematics: A Study in Cognitive History. Cambridge UP, 2003.
Ngai, Sianne. Ugly Feelings. Harvard UP, 2005.
Stein, Gertrude. “Are There Arithmetics.” The Gertrude Stein Reader, edited by Richard Kostelanetz, Cooper Square Press, 2002.
Wittgenstein, Ludwig. Zettel, edited by G.E.M. Anscombe and G.H. von Wright, translated by G.E.M. Anscombe, University of California Press, 1967.

About the Author
Kelly Krumrie is a writer and teacher. Her creative and critical writing can be found in journals such as echoverse, Annulet, DIAGRAM, and Black Warrior Review. Her first book, Math Class, will be published by Calamari Archive in 2022. She holds a PhD in English & LIterary Arts: Creative Writing from the University of Denver, and she is currently the Visiting Writer at Western Colorado University.